電験_自動制御No8_駆動サーボ系の伝達関数と増幅度の算出（ 1種 応用−昭和60年−問題4）

☆電験１種計算問題のバイブル（動画解説付きで安心して土台固めができます）☆

図は，他励直流電動機Mに歯車で結合された慣性モーメントJLと制動係数DLの負荷を駆動するサーボ系を示す。

ポテンショメータ1及び2で角度を電圧に変換しているが，その比例係数をkpとして，e1=kpθi，e2=kpθ0で表されるものとする。

また，電動機Mの回転子そのものの慣性モーメントをJM，制動係数をDM，電動機の逆起電力係数及びトルク係数をそれぞれke及びktとし，電機子巻線と増幅器との合成抵抗をRMとする。

さらに，歯車の歯車比は1：Nであり，歯車の慣性及び損失は無視できるものとする。

この場合，次の問に答えよ。

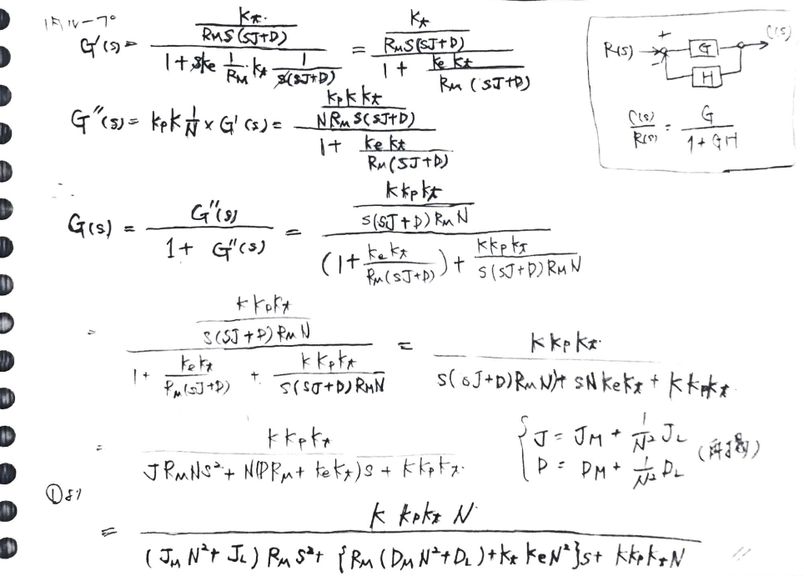
（１）このサーボ系における伝達関数G（s）＝θ0（s）／θi（s）を求めよ。

（２）このサーボ系において，θi をステップ関数状に変化させたときの θ0 の応答が非振動的でしかも最も速い応答（臨界減衰応答）を示すときの増幅器Aの増幅度Kを求めよ。

☆電験1種・2種の論説問題対策の決定版はこちらをクリック☆

☆電験１種計算問題のバイブル（動画解説付きで安心して土台固めができます）☆

☆電験１種計算問題のバイブル（動画解説付きで安心して土台固めができます）☆

電気主任技術者への道（計算編）の記事一覧へ